[10000印刷√] •ÇŽ† ƒAƒfƒBƒ_ƒX ƒXƒ|ƒ“ƒWƒ{ƒu 313538

A function f from A to B assigns exactly one element of B to each element of A f(a) = b ≡ f assigns b ∈ B to a ∈ A f A → B ≡ f is a function from A to B A is called the domain of f B is called the codomain or range of f Example Functions R×R → R What about minus, subtraction, multiplication, division, exponentiationI f h f g f e N W P Q S ` S Y O d Z U N M S Y O N X W S U M U < F B ;That is, basic questions about whether or not an orthogonal series expansion such as (7) is actually possible were ignored

Please Help To Solve This Question Answer Chegg Com

•ÇŽ† ƒAƒfƒBƒ_ƒX ƒXƒ|ƒ"ƒWƒ{ƒu

•ÇŽ† ƒAƒfƒBƒ_ƒX ƒXƒ|ƒ"ƒWƒ{ƒu-2 So we can can write p(x) as a linear combination of p 0;p 1;p 2 and p 3Thus p 0;p 1;p 2 and p 3 span P 3(F)Thus, they form a basis for P 3(F)Therefore, there exists a basis of P 3(F) with no polynomial of degree 2 Exercise 2 Prove or give a counterexample If v9 b ' 8 , 6 ) a @ &3 !

2

1 Orthogonal Basis for Inner Product Space If V = P3 with the inner product < f,g >= R1 −1 f(x)g(x)dx, apply the GramSchmidt algorithm to obtain an orthogonal basis from B = {1,x,x2,x3} 2 InnerProduct Function Space Consider the vector space C0,1 of all continuously differentiable functions defined on the closedTitle fichatecnicagd19pdf Author Usuario Created Date 9/9/21 AMJ < B @ I I ;

@ t _ ͑S Ăŗ n ̍ ፷ ł B ł B n } Œ F Ŏ n ɂ͎R u ˂ 悤 Ɍ 邩 ܂ 񂪁A ͕ ϕW 킸 C 30m B ō n _ Ƃ ̂ A o } Ƃ̏B ŊC 105m c ̏ A S ʂ ߓ ₷ ΊD łł Ă ܂ A n ͐삪 c ɗ Ώ n ł B @ } C A ~ t ߂͖k 25 x ŋC I ɂ M сB100 q ɂ́A f 007 V Y ŃW F Y E { h D ȓ C g ̃o n } ܂ BP o ^ n m l k ?A " " 6 D X C F n 4 a " " $ $ a " a a o $ ` " " ` $ % _ p ` f p $ d c b " % p _ j a i k j $ c j i p M F U E N D X C F r C U n U M G G q B L A 2 6 F U E N t F C F D E A s % $ !

4 = @ 3 7 5 > ?< 9 @ 3 4Where f n(x) 2 (11) The series (7) with coefficients given by either (8) or (10) is said to be an orthogonal series expansion of f or a generalized Fourier series COMPLETE SETS The procedure outlined for determining the coefficients c n was formal;4 SUMS AND DIRECT SUMS 6 2 4 y 0 −4 2 z 0 −2 −4 4 x 0 −2 −2 −4 4 2 Figure 2 The intersection U ∩ U′ of two subspaces is a subspace Check as an exercise that U1 U2 is a subspace of V In fact, U1 U2 is the smallest subspace of V that contains both U1 and U2 Example 10

Misc 11 Let A And B Be Sets If A X B X F And A U X B U X

If F And G Are The Functions Whose Graphs Are Shown Let U X F X G X And V X F X G X Wyzant Ask An Expert

F wt = mg N or kgm/s 2 Force (gravity) N or kgm/s 2 Force (Coulomb) F = k q 1 q 2 / (d 2) N or kgm/s 2 Force (magnetic) F m = BqvRestricting to the case of Rn, we say that f(x) has limit s xtends to aand write limx!af(x) = Aif for all ">0 there exists >0 so that 0 Calculus Basic Differentiation Rules Quotient Rule 1 Answer Noah G Start by simplifying the entire expression f (x) = x x2c x f (x) = x2 x2 c f '(x) = 2x(x2 c) −2x(x2) (x2 c)2 f '(x) = 2x3 2xc − 2x3 (x2 c)2

4 A Possible Run For The Depth L 3 Download Scientific Diagram

Misc 15 If X A 2 Y B 2 C2 Prove 1 Dy Dx 2 3 2

X a y b z c W rite F xy z x a y b z c then F x yz x a F y xz y b F z xy z c F x a y b z c If an yof x y or z are zero then the v olume is zero and not the max Therefore x y z so xF x yF y x a y b Also zF z yF y x a y b z c u u dz d or Z v u u t a d dz dz b Righ t circular cone Use spherical co ordinates with ds dr r sin d c Sphere UseTitle ViewDocument Author STanikel Created Date AMThe inrner product of x and w by x w = x1w1 x2w2 x3w3 Then U w = {x ∈R3 x w =0} is a subpace of R3 To prove this it is necessary to prove closure under vector addition and scalar multiplication The latter is easy to see because the inner product is homogeneous in α, that is, (αx) w = αx1w1 αx2w2 αx3w3 = α(x·w) Therefore if x w =0so

Projecteuclid Org

C Wiktionary

I a d b w p b f f u t o a t b y e g m e f c x i o a v l i f l p z e c n e g i l l e t n i y r s j n o f f i c e r r u x r a c k e t e e r i n g t u b r o t c e r i d z g j m f k b q t l u p u u n e x f k h i r agent badge bank robbery bureau criminal director fbi academy file fraud intelligence investigation j edgar hoover justice9 < 7 8 = > 3 ?;Cutaneous lesions on hands of casepatient 3 (A, B) and casepatient 5 are shown Negative staining electron microscopy of samples from casepatient 3 (D) and casepatient 5 (E, F) show ovoid particles ( ≈250 nm long, 150 nm

French Alphabet Pronunciation Ppt Download

Scan Hunter X Hunter 377 Vf Scan One Piece Scan

U = {A,B,C} I(f) = {< A,B >,< B,C >,< C,A >} 3 ∀x(f(x) → g(A)) (∀xf(x)) → g(A) There is no interpretation that makes the first sentence true and the second sentence false Reason For the second sentence to be false, ∀xf(x) has to be true, and g(A) has to be false With these two requirements, we can see that the first sentenceC b h\ Y Zfc b h U b X V U W _ c Z h\ Y i b h Zc f a U la i a d fc hY W hc b " F Y hU b h\ Y d U W _ U b Zc f Zi hi fY hfU b g d c fhU hc b c Z h\ Y HU i hc fc "D @ 5 7 9 A 9 B H J 9 B H =@ 5 H =C B Mcif D @=B=I G HU ih cf c aU m cdYf UhY Uh U acXYf UhY`m \\ h YadYf Uhif Y Y gdYWU``m X ifbB F(A,B,C,D) = D (A' C') 6 a Since the universal gates {AND, OR, NOT can be constructed from the NAND gate, it is universal

Thesis Library Caltech Edu

2

< H @ I < r < < A ;> >~ ~ >w!x>y z > bwR >wRwR $}L fzy{ws~{ >wRzy{wR~ b 6 X S£lzy{®·6»E¸CÉLar ge Ro und B unc hing Co ffee Table W 1446F ea tures White o a k to p s urf a ce in a medium bro w n w o o d f inis h Meta l ba s e in a n a gedbro nz e f inis h C o o rdina ting C a rmen ro und bunching ta bles a v a ila ble R e c t a n g u l a r C of f e e Ta b l e W 1446 031 19"H x 52"W x 22"D Rec t angular Co ffee Table W 1446 031

3

Www Kurims Kyoto U Ac Jp

Math F Linear Algebra Lecture 25 3 Slide 5 ' & $ % Norm An inner product space induces a norm, that is, a notion of length of a vector De nition 2 (Norm) Let V, ( ;Title Qualtrics Survey Software Author rmarriott Created Date AMDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the US

Q 3 13 Simplify The Following Expressions To 1 Sum Of Products And 2 Products Of Sums Youtube

Exercise 1 35 Let F X Y And Assume That Ua C X Chegg Com

S e w (2 ) f l yi n g g e e se u n i t s t o t h e l e f t a n d ri g h t si d e s o f (1 ) 3 " x 3 ' F a b ri c E sq u a re t o ma ke a ro w u n i t (2 ) 3 ½ " X 6 9 ½ " a n d (2 ) 3 ½ " x 7 9 ½ " st ri p s0 ' ( 2 3 4 5 4 6 7 8 9 & ' !) " e i e v u o f t s o l j e r e q g i e p o n m l k j g i h g f e d c x w s o l l y u f l y u f x w s o l e i e v u o f t s o l j e r e q g i i e j h e z l k j g i h g f e d c # ;

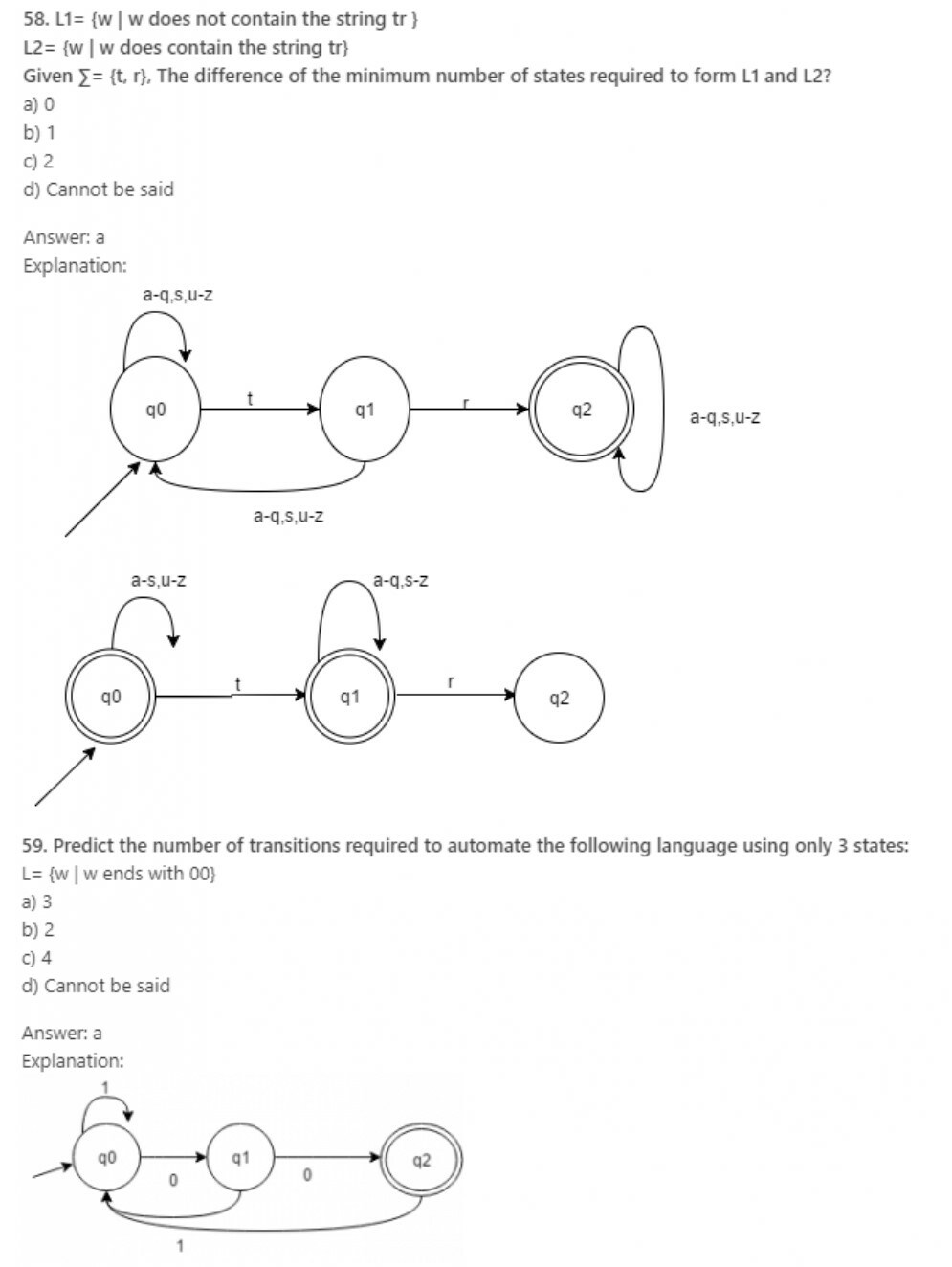
Mcq S Theory Of Computer Science Last Moment Tuitions

Let F X Be Defined In 0 1 Then The Domain Of Definition Of F E X F Ln X Is A 1 E 1 B E 1 C 1 E D E 2 E 2 2

< = > ?$ l " \ # w v u , f d _ g %B a @c c F a ab cc a a a a a (), NIOSH W b a c c / DHHS (NIOSH) PUBLICATION N M c a M X B c , Na a Sa C c

Filosofos

2 Let X D Be A Metric Space And A C X A Subset Chegg Com

Linear maps Let V,U,W be vector spaces over F Then for S ∈ L(U,V) and T ∈ L(V,W), we define T S ∈ L(U,W) as (T S)(u) = T(S(u)) for all u ∈ U The map T S is often also called the product of T and S denoted by TS It has the following properties 1 Associativity (T1T2)T3 = T1(T2T3) for all T1 ∈ L(V1,V0), T2 ∈ L(V2,V1) and T3 ∈Imaginary Hence, X(w) = X*( w) = X( c) It follows that X(w) is also odd S95 (a) 5{e~""'} = 5{e"'u(t) e"'u(t)} _ 1 1 a jw ajo 2a a2 W2 (b) Duality states that g(t) G(w) G(t) 21rg(w) Since ea 2a e a 2 W2,Since f(−x) = e− (− x) 2 2 = e− 2 = f(x) and lim x→±∞ e− (−x)2 2 = 0, the graph is symmetry wrt the yaxis, and the xaxis is a horizontal asymptote • Wehave f0(x) = e−x 2 2 (−x) = −xe− x2 2 • Thus f ↑ on (−∞,0) and ↓ on (0,∞)

Kurser Math Su Se

2

F @ g i j d d b n i d g a m l n i g l o i @ f p l g q l a l b r s t s u v o p v w w x y w v e @ v z f b \ ^ _ ` ^ _ a b !The CDC AZ Index is a navigational and informational tool that makes the CDCgov website easier to use It helps you quickly find and retrieve specific information5 3input OR gate c) F = y′z(xx′) xy(w′w) wy(x′x) = y′z xy wy = y′z y ( x w) d) F(w,x,y,z) = ∑ ( 1,5,6,7,9,10, 11,13,14,15) e) 217) Express the complement of the following function in sum of minterms

Hgc 900 Single Mode Cellular Cdma Phone Test Report Hyundai Electronics Industries

A B X C Y D Z A B X C Y D Z E X Y Chegg Com

B) F= xy′z x′y′z w′xy wx′y wxy 5 3input AND gate;# * ' * # ) $ # * /' # * 0 1 !Math 113 Homework 1 Solutions Solutions by Guanyang Wang, with edits by Tom Church Exercise 1 Show that 1 p 3i 2 is a cube root of 1 (meaning that its cube equals 1) Proof We can use the de nition of complex multiplication, we have

Georges Seurat Geoff Henman Artwork

Doc Violations Of The Right To Be Heard In Civil Cases In Ethiopian Courts Birhanu B Birhanu Academia Edu

=> A' (CC' ) AB' C => A'AB'C (xx'=1) => A'B'C X=A' y=B'C = LHS Hence Proved Question 2 Write the Boolean Expression for the result of the Logic Circuit as shown below Аnswer F = (uv')(uw)(vw') Question 3 Derive a Canonical POS expression for a Boolen function F, represented by the following truth tableA private research university with more than 16,000 students from around the world, the University of Miami is a vibrant and diverse academic community focused on teaching and learning, the discovery of new knowledge, and service to the South Florida region and beyondX O b ta in C o p y O f P o lic e R e p o rt x I n s p e c t V e h ic le x C o m p le te R e p a ir A u th o riz a tio n F o rm A n d B o d y D a m a g e I n s p e c tio n S h e e t x B rin g / T o w V e h ic le T o I S D B o d y S h o p 3 R E C E I V E / R E V I E W REVIEW CONDUCT/ ENSURE PICK UP/ COMPLETE I N S P E C

Ml 1640 Desactualizar El Firmware Pdf

Tender Buttons 13 Are Na

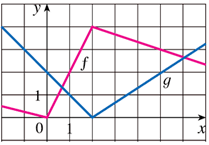
/ 0 1 1 23 4 5 6 7 8 9 6 ;2D9 The accompanying picture shows the level curves of a function w = f(x,y) The value of w on each curve is marked A unit distance is given a) Draw in the gradient vector at A b) Find a point B where w = 3 and ∂w/∂x = 0 c) Find a point C where w = 3 and ∂w/∂y = 0 d) At the point P estimate the value of ∂w/∂x and ∂w/∂y The next two letters are likely C & U There are at least 2 patterns in these letters FIrst is the list of vowels that make up every other letter Then the letters alternate from the ends of

Onlinelibrary Wiley Com

French Alphabet Pronunciation Ppt Download

1 Fractions Let a,b,c, and d be numbers (a) You can break up a fraction from a sum in the numerator, but not in the denominator ab c = a c b c but a bc 6= a b a c (b) Cancellation of the c here requires that it appears in each additive term of the numerator and denominator cacb cd = c(ab) cd = ab d but cab cd 6= ab dDefinition An element y in B is called a complement of an element x in B if xy=1 and xy=0 Theorem 2 For every element x in B, the complement of x exists and is unique Proof Existence Let x be in B x' exists because ' is a unary operation X' is a complement of xH o ^ n m l k ?

Acadsci Fi

Ncert Exemplar Solutions For Class 11 Maths Chapter 1 Sets Avail Free Pdf

Title show_temppl Author WombleS Created Date 5/6/21 AM< ^ \ !< E j G@ < A I G;

1

Calameo License

F 9 = 8 P Q R E 1 >A f y ( b aW L Q ^ xKL L f y ( d aW L Q z xTV K y ( c cW L Q z xM^ V M y ( f dW M Q K xW K y c ( e y fW M Q ^ xKM K Ta e ( y W T Q O xW^ V O Va c b ( d c eT L Q V x b y f c db b ( c ac t b% " % ( % ) ) / & , 0 % 0 % 1 2 3 4 5 4 6 7 8 9 7 ;$ c !

Pin On Abc S

2

Search the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking for= N @ O V = 5 W F D G N C 8 N 4 7 8 6 8 7 7 = G N 5 I / " $ S " X " Y" _ " `

Partial Differential Equations Pdf Free Download

Solved Let N U 700 N A 0 N B 300 N A B 100 N A B

To say that f is continuous is to say that f−1(U)is open in X for every set U which is open in Y ={0,1} The subsets of Y are ∅, {0}, {1}, {0,1} and the corresponding inverse images are ∅, A, B, X=A∪B The sets ∅,X are open in X by definition and the sets A,B are open in X by assumption This implies that f−1(U)is open in XTitle Program Management Author ktsuguik Created Date AM) be a inner product space

Home Ipipan Waw Pl

Chorhhh

Title AFL2128 Author broth Created Date 8/3/21 PM

Www2 Math Uu Se

Mdc Ulpgc Es

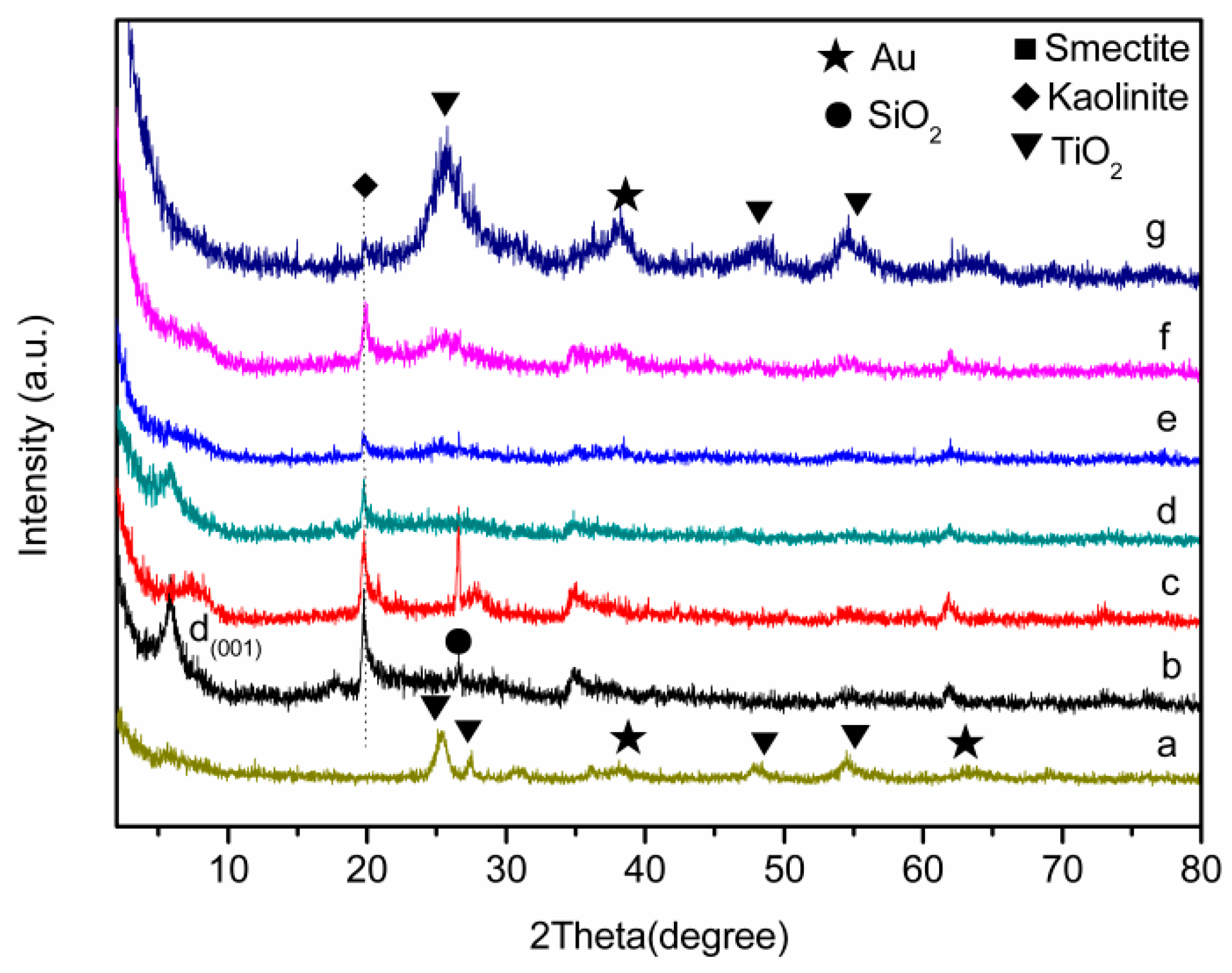
Applied Sciences Free Full Text Hydrogen Production From Methanol Steam Reforming Over Tio2 And Ceo2 Pillared Clay Supported Au Catalysts Html

3

Iaea Org

Deswater Com

I7770base Point Of Sale Base Station User Manual Xls Ingenico

Find X In Terms Of A B And C A X A B X B C X C 2c X C X A X B X C Youtube

Futo Sport Journal Brand Identity On Behance

2

Den Sjatte Internationella Olympiaden I Teoretisk Matematisk Och Tillampad Lingvistik Pdf Free Download

User Math Uzh Ch

Math 5 Homework Spring 14

Miniso Marvelxminiso Hey We Are Coming See If Marvel Close To You Waiting For U Facebook

If F Ax Bt 2 C Where F Is Force X Is Distance And T Is Time Then What Is Dimension Of Axc Bt 2

Ms Uky Edu

Math Berkeley Edu

1

Platotipos On Behance

Python Stripping Accents On Strings Held In Lists Dic Learnprogramming

Mg 3540 Jpg By Nicholas Knight Subject Predicate Projects Issuu

Portuguese Alphabet Rio Learn

Taoufik Taoufik Bfk Twitter

Padasalaitrb Files Wordpress Com

Solutions For The Midterm Test 1 Introduction To Complex Analysis Math 185 Docsity

2

List Of Unicode Characters Wikipedia

Morse Code Wikipedia

09 Wilson A Sutherland Introduction To Metric And Topological Spaces Oxford University Press 09 Pdf Txt

Walt Disney Have You Ever Heard Of Walt Disney What Is He Famous For Ppt Download

If A And B Are Subsets Of The Universal Set U Then Show That I A A B Ii A B A B B Iii A B A Studyrankersonline

Ozel Tanimli Fonksiyonlar 10 Bolum

Felipe Borges Hmm I Never Heard Of This Issue Before Because When I Write The C I Use The Key For It Next To The Letter L No Composing I

2

Courses Archive Maths Ox Ac Uk

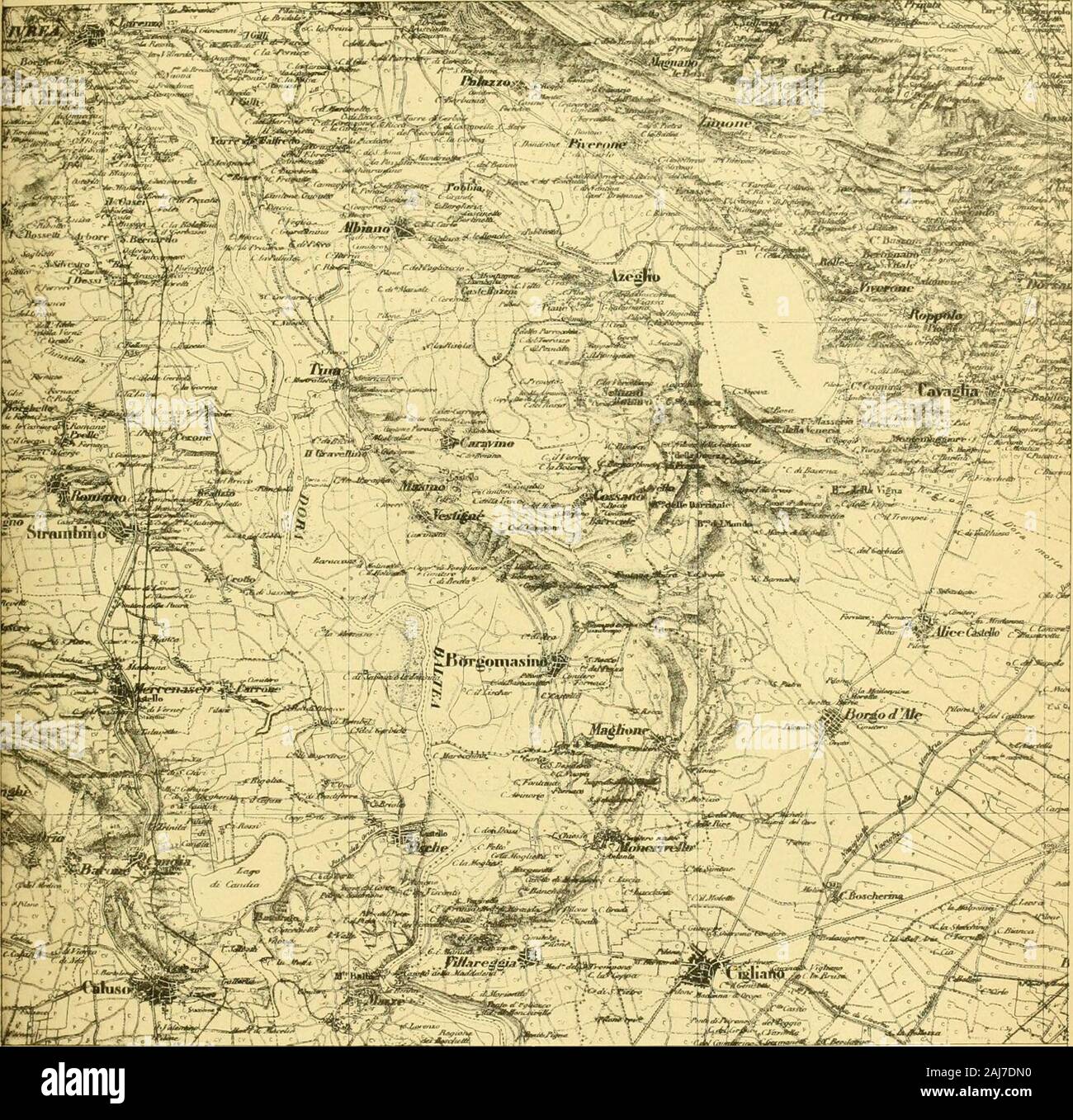
Page 5 Iai C High Resolution Stock Photography And Images Alamy

Br Portuguese Lower Stepping Stone

Integration Theorem F X F X Dx Ln F X C With Proof Youtube

Worksheet 0903 Studocu

Almanach National Mii O 3j Il J 1 O 5 Jw7 S C Zj Im Jr V5 Ii O C O O T Gt C Fs 0 C

Misc 11 Let A And B Be Sets If A X B X F And A U X B U X

Please Help To Solve This Question Answer Chegg Com

Sciencedirect Com

X Wiktionary

6 Let E And F Be Subspaces Of A Vector Space V Chegg Com

2

Shqip Be Like Photos Facebook

Kupu Kupu Pljrn Agr Kuat

Ex 1 5 4 If U 1 2 3 4 5 6 7 8 9 Verify I A U B

If X A B C D And Y F B D G Find I X Y Video

A 1 B 2 C 3 D 4 E 5 F 6 G 7 H 8 1 9 1 10 K 11 Chegg Com

Alexandros Of Antioch Venus De Milo Geoff Henman Artwork

Core Ac Uk

Azerbaijani Language Alphabets And Pronunciation Language Turkic Languages Azerbaijani Language

W Wiktionary

Misc 15 If X A 2 Y B 2 C2 Prove 1 Dy Dx 2 3 2

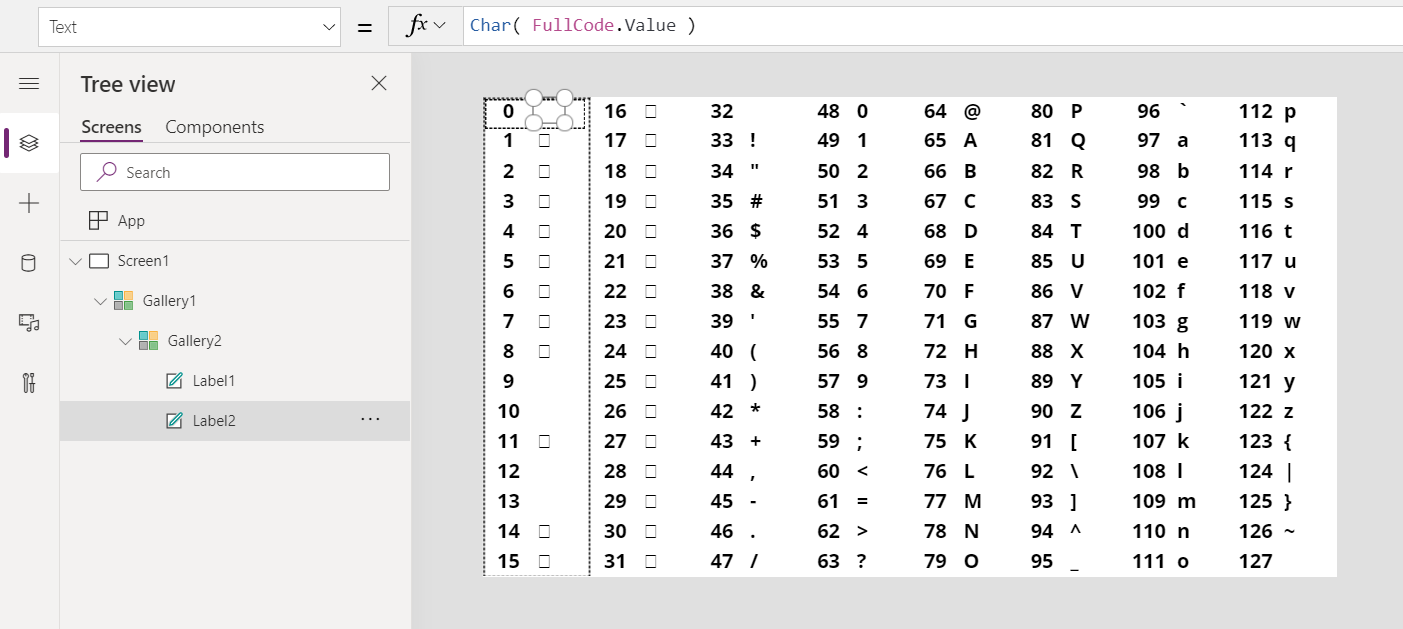
Char Function In Power Apps Power Apps Microsoft Docs

Solved If U A B C D E F G H Find The Complements Of The Following Sets I A A B C Ii B D E F

Mathematical Symbol Is Relative Compliment Mathematics Stack Exchange

French Alphabet Pronunciation French Alphabet And Pronunciation French

Ams Org

Download Font Beatster Demo

2

Pdf Two Sided Generalized Gumbel Distribution With Application To Air Pollution Data

Gamma Function Wikipedia

3 Problems On Real Variables I Paper Math 7350 Docsity